Avez-vous déjà entendu parler de la symétrie centrale ? Si non, ce cours est fait pour vous !
Symétrie centrale, en bref
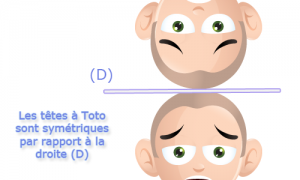
Prenons l’image suivante :
Nous avons ici une symétrie par rapport à une droite. En effet c’est comme si nous avions utilisé un miroir.
Mais et symétrie centrale c’est quoi alors ? Ce n’est pas la même chose ?
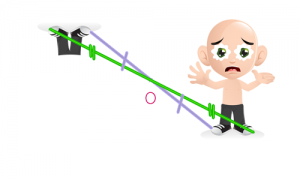
Toto, nous allons voir maintenant la symétrie par rapport à un point et non une droite 😉
Tout d’abord, dessinons les jambes de Joe, l’ami de toto, grâce à la symétrie de l’image de Joe par rapport au point O :
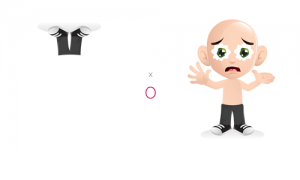Super, nous avons dessiner ses jambes.
Dessinons maintenant tout son corps !
Savez-vous comment nous nous sommes pris pour faire ce dessin ? Pas difficile :
Nous avons en effet créer chaque point de l’image en traçant un segment passant par le point O et tel que O soit le milieu du segment, d’où symétrie centrale ;).
Pour conclure, donnons la définition :
Soit un segment [AB] et son milieu I, on dit que A et B sont symétriques par rapport à I.
Propriétés à connaître par cœur
Vous avez compris à quoi sert la symétrie centrale, et comment l’appliquer. Nous allons maintenant évoquer les propriétés de celle-ci. Elles doivent impérativement être apprises par cœur 😉
Milieu et symétrie
Si un segment a pour milieu le point O, alors les extrémités de ce segment sont symétriques par rapport à O.
Symétrique d’un segment
L’image d’un segment par une symétrie centrale est un segment de même longueur.
La symétrie centrale conserve les longueurs.
Symétrique d’une droite
L’image d’une droite par une symétrie centrale est une droite parallèle.
Figures symétriques
Deux figures symétriques par rapport à un point O ont le même périmètre et la même aire.
La symétrie centrale conserve les périmètres et les aires.
Angles symétriques
Deux angles symétriques par rapport à un point O ont la même mesure.
La symétrie centrale conserve la mesure des angles.
Cercles symétriques
Deux cercles symétriques par rapport à un point O ont des centres symétriques par rapport à O et des rayons égaux.
