Ce cours est l’un des plus importants cette année. Vous allez voir plusieurs figures que vous retrouverez dans les prochains années. Alors soyez attentifs 😉
Le parallélogramme, trop parallèle celui-là
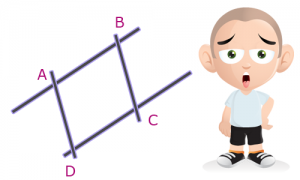
C’est simple, prenez 2 droites parallèles. Maintenant prenez une droite (D) qui coupe ces deux droites parallèles. Ajoutez (presque) n’importe où une droite (D’) qui soit parallèle à (D). Vous obtenez un parallélogramme 🙂
Compliqué ? Voyons cela plus simplement :
Un parallélogramme est un quadrilatère qui a ses côtés opposés parallèles.
Mais au fait, c’est quoi un quadrilatère déjà ? C’est tout simplement un polygone qui a 4 côtés.
Ne me demandez pas ce que c’est qu’un polygone 🙂
Vous ne savez vraiment pas ? Eh bien ce n’est tout simplement qu’une figure géométrique plane.
Certain diront que c’est un dessin 🙂
Pour résumé, un parallélogramme, c’est un polygone qui a 4 côtés et dont ses côtés opposés sont parallèles.
Une petite image pour comprendre tout ça 🙂 :
J’espère que vous avez remarqué que les côtés AB = CD et que BC = AD.
Mais avez-vous remarqué une symétrie… ? 🙂
Je vous laisse chercher un instant.
C’est bon vous avez trouvé ?
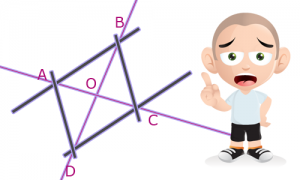
Et, voici :
Et, oui ! O est le symétrique de A par rapport à C. Donc O est le milieur de AC ! De même, O est le symétrique de B par rapport à D. Donc O est le milieur de BD.
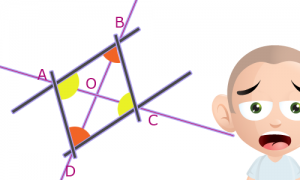
Avez-vous maintenant remarqué une histoire d’angle ?
Je dirais même plus ! Ne semble-t-il pas que certains angles sont égaux ?
En effet, les angles opposés sont égaux !
Encore une petite devinette, nous avons une symétrie de centre O avec les angles de ce parallélogramme.
Pouvez-vous l’identifier ?
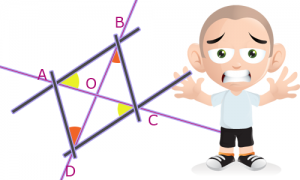
Eh oui, on a dans la symétrie de centre 0 :
L’angle BAC a pour symétrie l’angle ACD. Donc l’angle BAC = l’angle ACD.
De même l’angle CBD a pour symétrie l’angle ADB. Donc l’angle CBD = l’angle ADB.
Voilà pour nos amis les parallélogrammes !
Le rectangle, il ne connait qu’un seul angle
Le rectangle ne connait qu’un seul angle : l’angle droit à 90°.
Ayant vu le parallélogramme, nous allons aller un peu plus vite sur ce cours.
Partons là encore de la définition d’un rectangle :
Un rectangle est un quadrilatère qui a ses 4 angles droits.
Donc pour construire un rectangle, je prends 4 segments, et je forme un rectangle si les 4 angles de mon polygone sont des angles droits !
Vous avez sûrement remarqué que s’il a 4 angles droits, ses côtés opposés sont parallèles. C’est donc un parallélogramme ! Il a donc les mêmes propriétés dit plus haut.
Le losange, un symbole
Alors ici la particularité d’un losange, c’est tout simplement qu’il a ses 4 côtés de même longueur (ce que n’a pas un rectangle, sinon ce serait un carré mais nous y reviendrons ;)).
Donc la définition, c’est bien celle-ci :
Un losange est un quadrilatère qui a ses 4 côtés de la même longueur.
Un losange est aussi un parallélogramme car il a ses 4 côtés parallèles. Il dispose donc des mêmes propriétés citées plus haut.
Le carré, il va te mettre la tête au carré !
Alors un carré c’est quoi ? Je suis sûr que tout le monde doit avoir son idée 🙂
Eh bien nous l’avions dit plus haut :
Un carré est un quadrilatère qui a ses 4 côtés de la même longueur et qui a 4 angles droits.
C’est là encore un parallélogramme ;).