Ce cours est l’un des plus simple, mais soyez attentifs !
Qu’est ce qu’un triangle ?
Il y a un début à tout ! Même si vous savez ce qu’est un triangle, je vous invite à lire cette partie, ce ne sera pas très long 😉
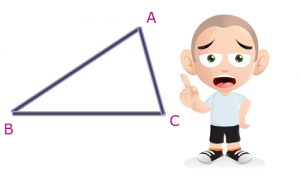
Tout d’abord un triangle est constitué de trois points. On utilisera dans ce cours à chaque fois les points nommés A, B et C.
Prenez donc 3 points (de préférence non alignés), dessinez les sur un papier. Tracez les trois droites passant par ces points 2 à 2.
Les segments obtenus forme notre triangle :
L’inégalité triangulaire, c’est trop fort !
Ne tournons pas à côté du pot ! Vous n’avez que cette formule à apprendre par cœur :
AB ≤ AC + BC
Cela veut dire quoi ?
Eh bien tout simplement que quelque soit le segment de votre triangle il sera toujours inférieur ou égale à la somme des deux autres. D’ailleurs, il est le plus souvent strictement inférieur à la somme des deux autres.
Toto, j’ai une question pour toi : Saurais-tu quand est-ce qu’on a AB = AC + BC ?
Allez ce n’est pas compliqué 😉
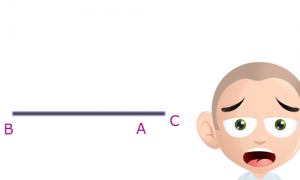
Réponse : (J’espère que tu avais trouvé) c’est lorsque les trois points A, B et C sont alignés !
Quelques bonnes propriétés pour nos triangles
Symétrie centrale
Hypothèse :
- ABC est un triangle quelconque.
- I est le milieu de [AB]
- J est le milieu de [BC]
- X est le symétrique de C par rapport à I
- Y est le symétrique de A par rapport à J
Propriété à connaître :
Les symétriques des points A et C par rapport au point I sont respectivement B et X.
Le symétrique de la droite (AC) par rapport au point I est donc la droite (BX), et (AC) // (BX).
Montrer que des points sont alignés
Hypothèse :
- (BX) // (AC)
- (BY) // (AC)
Conclusion :
(BX) // (BY)
Ces deux droites (BX) et (BY) ayant en commun le point B, on dit qu’elles sont confondues : X, B et Y sont donc alignés !
La somme des angles dans un triangle
Propriété à connaître :
Quelque soit notre triangle ABC, la somme des mesures des trois angles d’un triangle est égale à 180°.
Mesure des angles pour un triangle équilatéral
Propriété à connaître :
Dans un triangle équilatéral , il faut savoir que chaque angle mesure 60°.
Quelques droites particulières pour le triangle
Hauteur
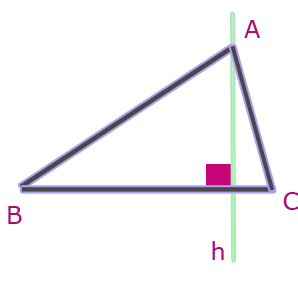
Qu’est ce qu’une hauteur ?
Prenons un triangle quelconque ABC, une hauteur est une droite passant par un sommet du triangle et perpendiculaire au côté opposé.
Qu’est ce qu’un sommet et que veut dire perpendiculaire ?
Un sommet est tout simplement soit le point A, soit le point B ou soit le point C.
Perpendiculaire… Vous devriez déjà savoir ça ! Deux droites sont perpendiculaires si la mesure de l’angle formé par ces droites est égale à 90°.
Médiatrice
Il y a deux mots importants à retenir quand on parle de Médiatrice :
– Milieu
– Perpendiculaire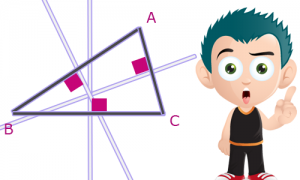
En effet une médiatrice d’un segment passe par le milieu de ce segment et est perpendiculaire à celui-ci. Ce qui se traduit pour un triangle en 3 médiatrices possibles :
Médiane
Là c’est différent, il faut retenir les mots suivants :
– Milieu
– Sommet
Eh oui dans un triangle ABC, une droite passant par l’un des sommets et passant par le milieu du côté opposé s’appelle une médiane.
Voilà pour ce qui est de l’essentiel de notre cours !